ETL 1110-1-175
30 Jun 97
This distribution is a function of c, and, to be com-
pletely defined, needs to be known for all values of
c. The distribution is used to make evaluations
such as: suppose that we have no measurement of
concentration of a certain contaminant at x, but the
distribution is known, and a threshold value of
c = 8 mg/l is of interest. If P [Z (x) # 8] ' 0.60 ,
then, if a measurement were made at x, there is a
60-percent chance of obtaining a value less than or
equal to 8 mg/l. The distribution also may be used
to calculate other probabilities, such as the proba-
bility of obtaining a value in some specified
interval.
(3) An important concept to keep in mind in
all geostatistical applications is the support of the
regionalized random variable. The support of Z(x)
is the in situ geometric unit represented by an
individual sample. For example, in a soil contami-
nation study, sample Z(x) might represent the con-
centration of a contaminant in a vertical soil core
0.1 m in diameter and 1 m in length, and centered
at location x. Thus, even though Z(x) is defined at
a particular point, it is representative of a volume
of soil. Changing the support of Z(x) will usually
change its probability distribution. Therefore, the
observations in a geostatistical analysis should all
have the same support. The method called point,
or punctual, kriging, described in section 2-4, is
designed to predict values of Z(x) with the same
support as the sample data.
(4) A concept closely related to support is that
of estimation block, which is a geometric unit
larger than the support of a single observation, for
which a single representative value is desired. For
example, in the above soil contamination study, it
may be necessary to estimate the average concen-
tration of the contaminant in a truckload of soil
excavated from a block 6 m long, 6 m wide, and
0.3 m thick. Using a method called block kriging,
also described in section 2-4, the block average can
be predicted based on individual measurements.
(5) Although the distribution of Z(x) com-
pletely characterizes Z(x) at any particular loca-
tion, this distribution indicates nothing about the
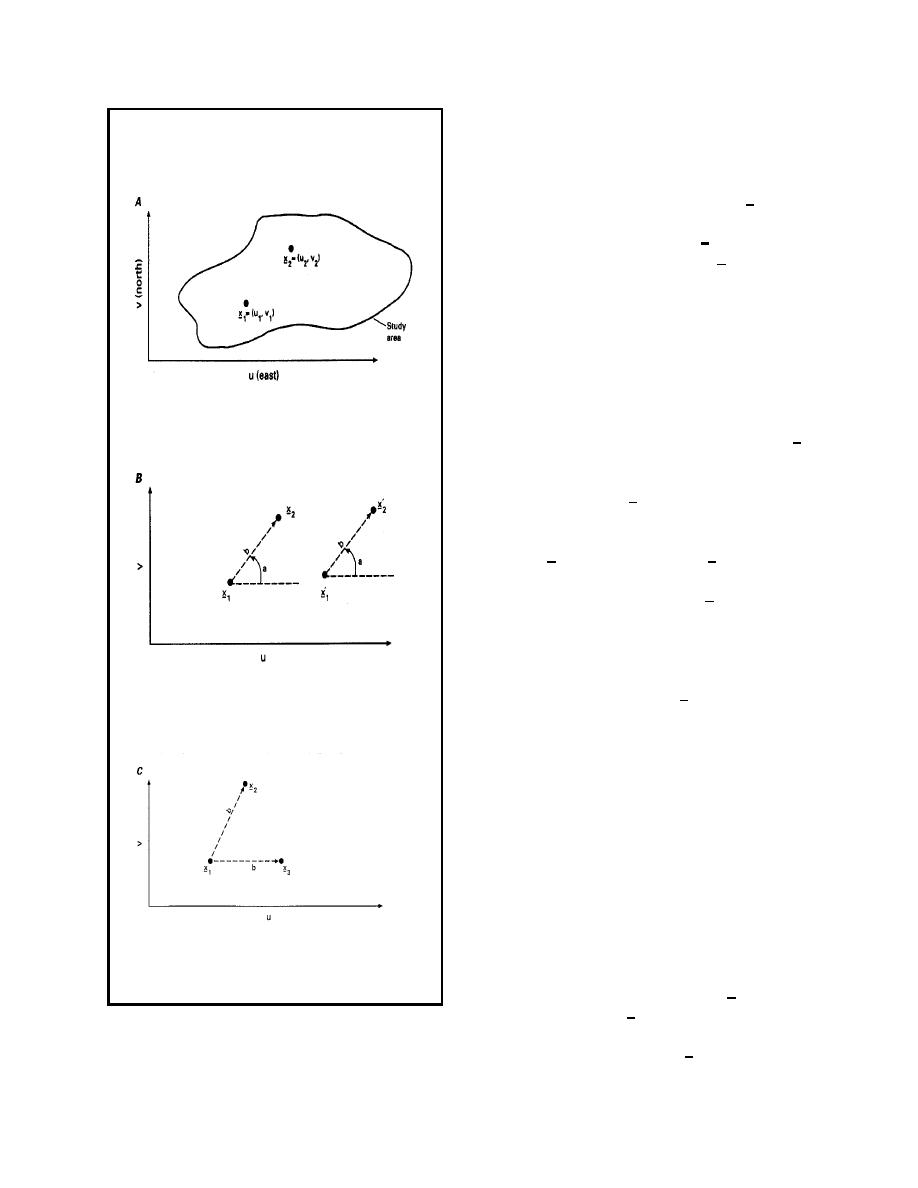
Figure 2-1. Diagrams showing A, hypothetical
relations among the values of Z(x) at different
study area; B, stationary covariance function; and
C, isotrophic covariance function
2-2




 Previous Page
Previous Page
