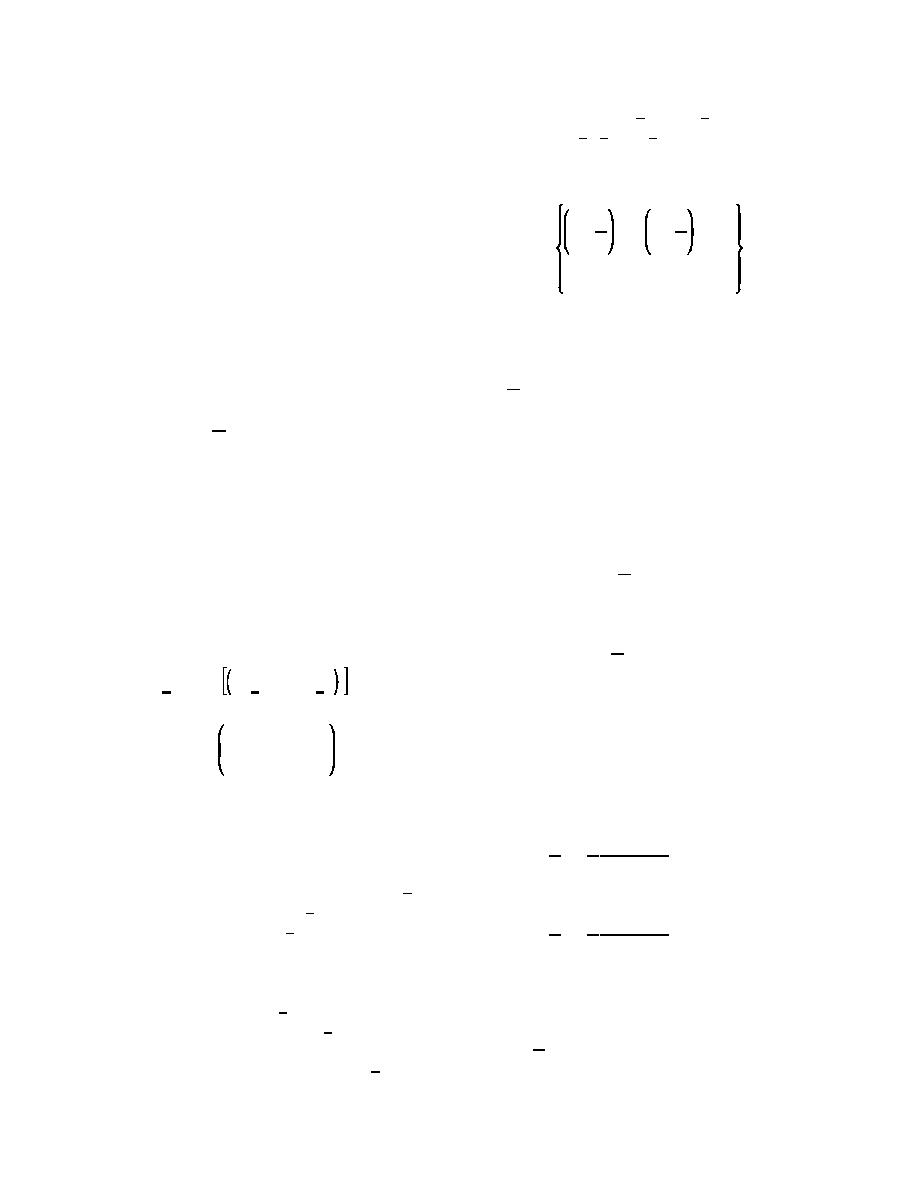
ETL 1110-1-175
30 Jun 97
on n=2 measurements Z(x1) and Z(x2), where the
equivalent to j wi = for any , which holds
n
three locations (x0, x1, and x2) are distinct. Using
i=1
Equations 2-23 and 2-28, note that the correlation
if and only if j wi = 1 . Therefore, all linear
n
function is
i=1
unbiased estimators need to have weights that sum
g
h
1&
exp & 3 , h > 0
to one. There are many sets of weights that satisfy
s
r
D (h) =
(2-37)
this condition, including the set with all the weights
equal to 1/n, as in the sample mean, Equation
h=0
1,
2-34. However, the unique set of weights that
minimize the prediction variance (Equation 2-33)
can be shown to satisfy the following set of n+1
For illustrative purposes, suppose that
ordinary kriging equations (Chapter 12, Isaaks
and Srivastava (1989)):
g
= p, 0 # p # 1
(2-38)
s
j wj Dij %
n
8
(2-35a)
= Di0, i=1, 2 ..., n,
s
where p is a fixed proportion. The quantity p is
j=1
sometimes referred to as a relative nugget.
j wj = 1
n
(2-35b)
(b) The ordinary kriging Equations 2-35a and
j=1
2-35b are given by
where Dij = D(hij) is the correlation between obser-
8
w1 % w2 D12 %
= D10
vations i and j, hij is the distance between locations
(2-39a)
s
i and j, and 8 is a coefficient resulting from the
constrained optimization. Furthermore, the
resulting ordinary kriging variance is
8
w1D12 % w2 %
= D20
(2-39b)
s
2
^
2
Fk (x)0 = + Z (x ) & Z (x )
0
0
(2-36)
w1 % w2 ' 1
(2-39c)
= s 1 & j wjDj0
n
&8
j=1
These three equations have three unknowns: w1,
w2, and 8; the solution is
(c) The system of Equations 2-35a and 2-35b
can easily be solved for the wi's and 8, after which
1 D10 & D20
1
the kriging variance can be obtained from Equa-
%
w1 =
(2-40a)
2 1 & D12
tion 2-36. Note that the ordinary kriging variance
2
changes depending on the prediction location x0,
even though the variance of Z(x0) itself (Equa-
1 D10 & D20
tion 2-6) is constant for all x0.
1
&
w2 =
(2-40b)
2 1 & D12
2
(2) Example 1.
and
(a) Let the mean of Z(x) satisfy Equation 2-30,
and suppose that the residual Z*(x) (Equa-
s
8=
(D10 % D20 & D12 & 1)
tion 2-16) has an isotropic exponential variogram
(2-41)
(Equation 2-23). Consider predicting Z(x0) based
2
2-11




 Previous Page
Previous Page
