ETL 1110-2-544
31 Jul 95
4-3. Constitutive Law and Material Properties
Chapter 4
Seepage Problems
a. Darcy's law. The constitutive relationship in
most finite element codes is based on Darcy's law.
Darcy's law states that the velocity of the fluid is
proportional to the hydraulic gradient. The constant of
Seepage problems involve the analysis of the flow of
proportionality in this relationship is termed the
groundwater through porous media such as soil and
coefficient of permeability. This coefficient is a
rock. Geotechnical engineers typically perform
parameter which is material dependent. Most finite
seepage analyses as part of the design process for
element codes are capable of handling materials having
embankment dams, levees, and river structures such as
anisotropic permeabilities.
locks and dams.
The coefficient of permeability is typically estimated in
three different ways:
4-1. Results and Uses of Seepage Analyses
(1) Sampling and laboratory testing. Sampling
The principal quantity solved for in a finite element
and laboratory testing where samples retrieved from a
solution of a seepage problem is the pressure head at
field exploration program are sent to the laboratory
each nodal point in the finite element mesh. All flow is
where permeability tests can be performed. The two
assumed to occur through the pore spaces of a rigid
most common types of laboratory permeability tests are
soil skeleton. From these heads, the quantity and
the constant head and falling head types of tests.
velocity of flow, and hydraulic gradients at any point
in the system can be determined. Flow nets can be
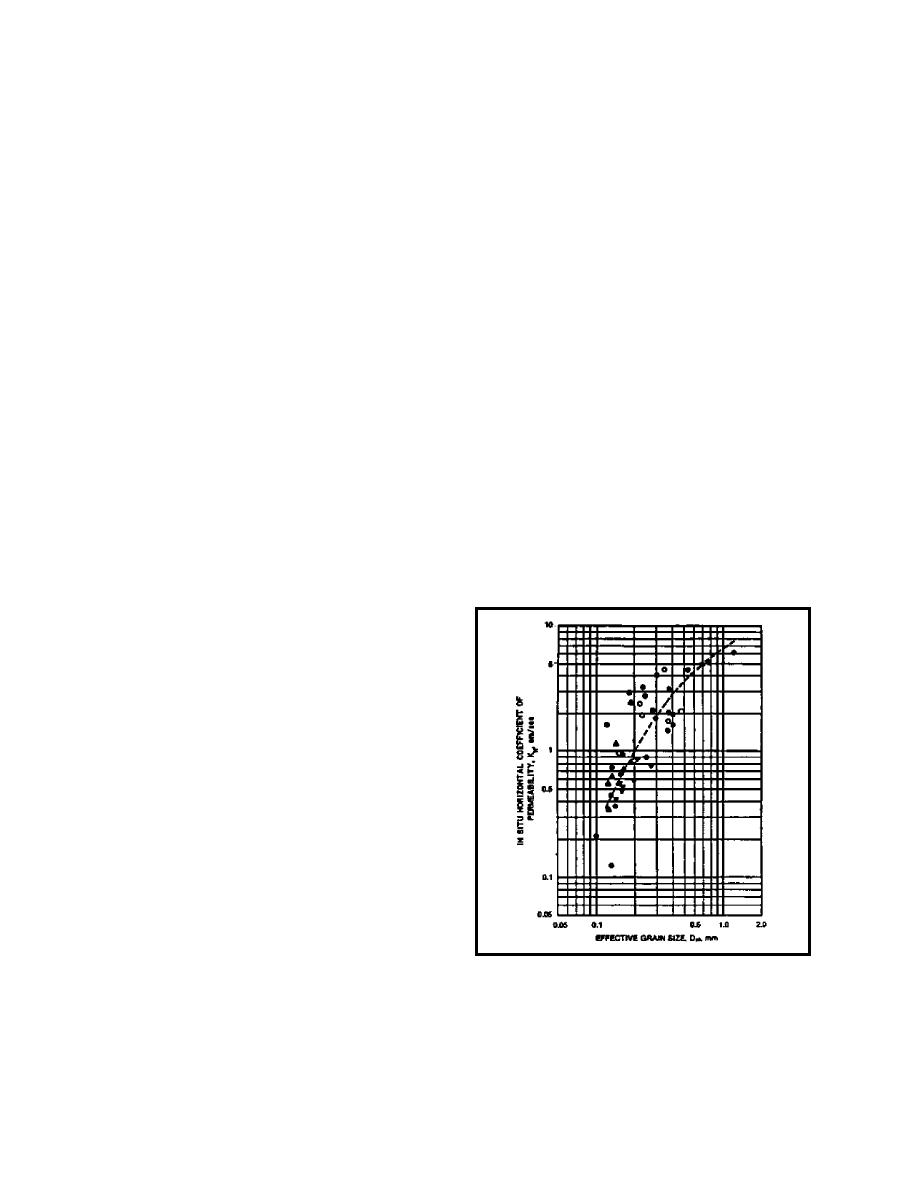
(2) Correlations with grain-size distribution. For
constructed from the finite element results to help the
example, the Lower Mississippi Valley Division of the
design engineer interpret the results.
Corps of Engineers has correlated the grain-size
distribution of sands in the Lower Mississippi Valley to
the coefficient of permeability. This relationship is
4-2. Types of Seepage Analyses
shown in Figure 33.
a. Seepage problems. Seepage problems can be
classified according the type of flow conditions
presumed to exist for the analysis. The analyses of
most seepage problems for engineering projects are
performed under the assumption of steady-state flow
conditions. This assumption implies that all conditions
affecting the flow of water through the system are the
same at all times, hence the solution is independent of
time. In contrast, transient solutions to seepage
problems, performed less frequently, are time-
dependent as factors such as changing headwater and
tailwater levels and the flow of water into partially
saturated soils can be accounted for in this type of
analysis.
b. Confined or unconfined seepage problems.
Seepage problems can also be classified as confined or
unconfined depending on the boundary conditions
presumed to exist. In confined flow problems, the
locations of all boundaries are known and fixed.
Unconfined flow problems must have at least one
impervious boundary and a free surface boundary. The
location of the free surface boundary (phreatic surface)
Figure 33. Relationship between in situ horizontal
permeability and effective size
is unknown and must be determined as part of the
solution. Boundary conditions are presumed to be
impervious to flow.
A-26




 Previous Page
Previous Page
