ETL 1110-2-547
30 Sep 95
g E Xi % FX & g E Xi & FX
that of the continuous random variable. Having only a
MY
i
i
'
few values over which to integrate, the moments of the
2 FX
M Xi
performance function are easily obtained. A simple
i
and straightforward point estimate method has been
proposed by Rosenblueth (1975, 1981) and is
When the above expression is squared and multiplied
summarized by Harr (1987). That method is briefly
by the variance, the standard deviation term in the
summarized below.
denominator cancels the variance, leading to
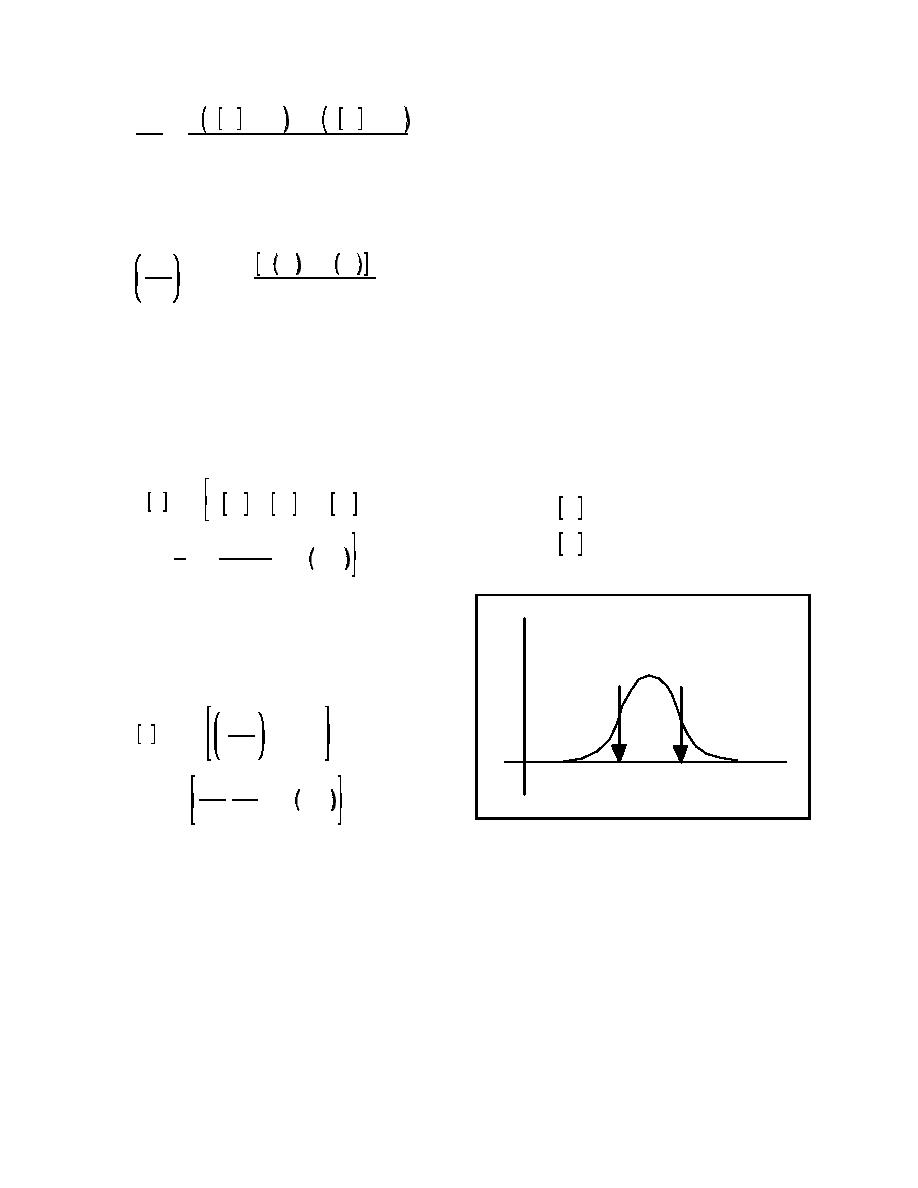
(1) Independent random variables. As shown in
g X% & g X&
2
2
MY
Figure B-3, a continuous random variable X is
Var X '
M Xi
represented by two point estimates, X+ and X-, with
2
the two point estimates and their probability concen-
where X+ and X- are values of the random variable at
trations form an equivalent probability distribution for
plus and minus one standard deviation from the
the random variable, the two P values must sum to
expected value.
unity. The two point estimates and probability con-
centrations are chosen to match three moments of the
(2) Correlated random variables. Where random
random variable. When these conditions are satisfied
variables are correlated, the solution is more complex.
for symmetrically distributed random variables, the
The expression for the expected value, retaining
point estimates are taken at the mean plus or minus one
second-order terms is:
standard deviation:
E Y ' g E X1 , E X2 , ... E Xn
Xi% ' E Xi % FX
i
Xi& ' E Xi & FX
2 j M Xi M Xj
M2 Y
1
Cov Xi Xj
i
%
However, in keeping with the first-order approach, the
second-order terms are generally neglected, and the
expected value is calculated the same as for
independent random variables. The variance,
f(x)
P+
P-
however, is taken as:
Var Y ' j
2
MY
Var Xi
M Xi
x
x-
x+
%2j
MY MY
Cov Xi Xj
M Xi M Xj
Figure B-3. Point estimate method
where the covariance term contains terms for each
possible combination of random variables.
For independent random variables, the associated
probability concentrations are each one-half:
b. Point estimate method. An alternative method
to estimate moments of a performance function based
Pi% ' Pi& ' 0.50
on moments of the random variables is the point
estimate method. Point estimate methods are pro-
cedures where probability distributions for continuous
Knowing the point estimates and their probability
random variables are modeled by discrete "equivalent"
concentrations for each variable, the expected value of
distributions having two or more values. The elements
a function of the random variables raised to any
of these discrete distributions (or point estimates) have
power M can be approximated by evaluating the
specific values with defined probabilities such that the
function for each possible combination of the point
first few moments of the discrete distribution match
estimates (e.g., X1+ , X2- , X3+ , Xn- ), multiplying each
B-9




 Previous Page
Previous Page
