ETL 1110-2-563
30 Sep 04
norm
Stiff-to-Rigid
y
Wall
Global Axis
par
Vnorm
θ
s
l Axi
Loca
VoxVy
Voy
Vx
x
θ
Towboat
Vpar
Figure E-1. Barge train and velocity vector transformation from local (barge) to global (wall) axis
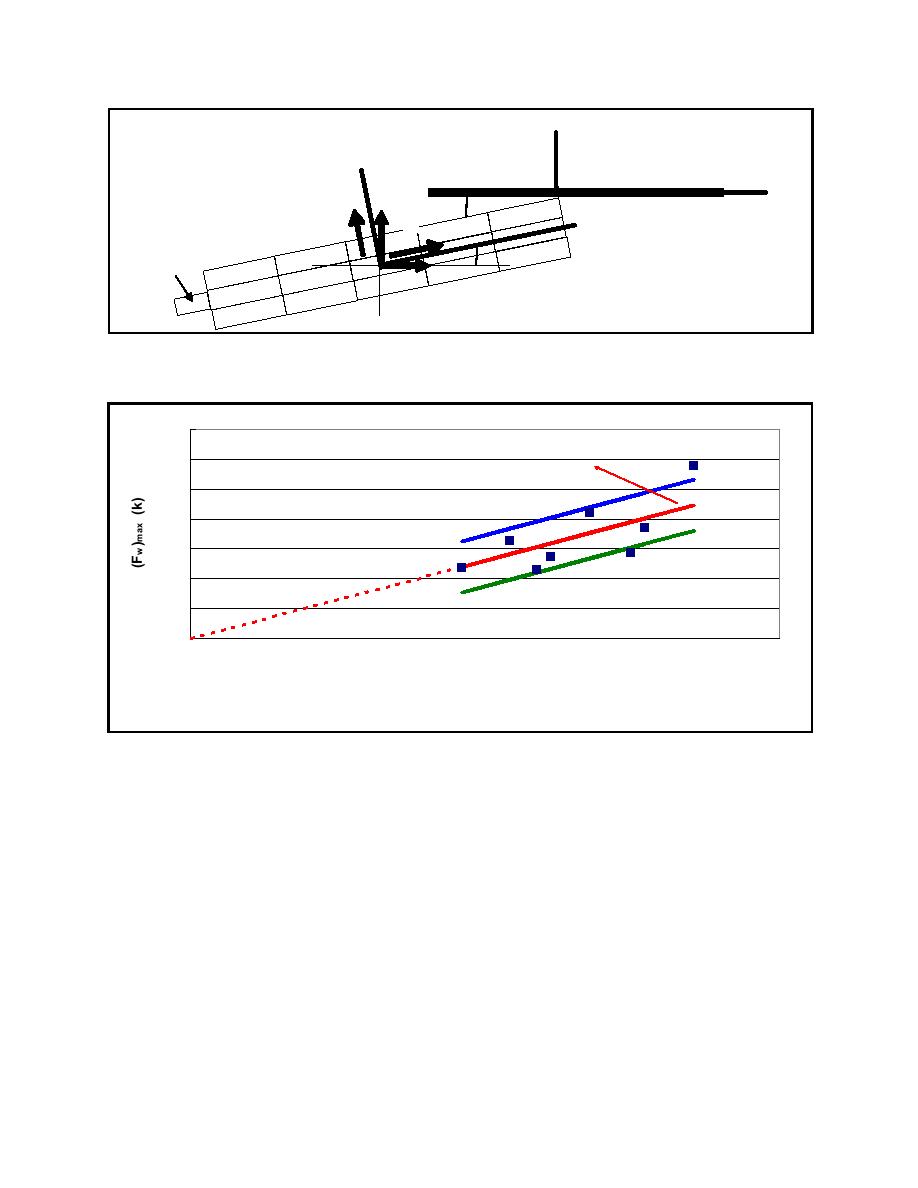
700
(Fw)max = 0.435(mvsinθ)
600
(Average)
500
(Fw)max = 0.435(mvsinθ)+85.328
400
(Average + SE)
300
200
(Fw)max = 0.435(mvsinθ)-85.328
100
(Average - SE)
0
0
200
400
600
800
1000
1200
Linear Momentum Normal to the Wall (k-s)
(mvsinθ)
Figure E-2. Empirical correlation between (Fw)max and linear momentum normal to the wall
impact force normal to the wall. This correlation is based on low-velocity, shallow-impact (up to
21.1 deg) experiments that, by definition, do not account for factors that manifest themselves at higher
velocities. Additionally, no damage occurred to the barge train, and no lashings broke during these eight
impact experiments. Therefore, it is deemed that this empirical method is applicable to a barge train that
has a velocity normal to the wall up to and not exceeding 0.17 m/sec (0.57 ft/sec (0.6 km/hr (0.39 mph)))
with no damage occurring during impact events, for impact angles up to 21.1 deg, for a barge train with a
linear momentum normal to the wall between 2.9 and 4.6 MN-sec (649.84 and 1,025.48 k-sec). The
equation to determine the maximum force normal to the wall using the empirical correlation is
(Fw)max = 0.435*m*(V0x *sin θ + V0y ∗ cos θ)
where the units for the mass, velocity, and maximum Fw are k-sec2/ft, ft/sec, and kips, respectively. Note
that no hydrodynamic added mass is assigned to m when using this relationship.
E-2




 Previous Page
Previous Page
