ETL 1110-2-540
30 Sep 96
measurement estimates the total rainfall over the area
The number of gages required depends on local
!
represented by that gage. For example, if the raingage
conditions. Areas of higher rainfall variability gener-
accurately measures rainfall at a point but that measurement
ally require higher numbers of gages to estimate rain-
is an inconsistent estimator of areal rainfall, the gage has
fall over a watershed adequately. Mountainous areas
little value. However, if the rain gage measurement
require more gages than flat lands. Areas subject to
consistently estimates areal rainfall, the measurements are
convective storms require more gages than areas
highly valuable, even if the point measurement is inaccurate.
subject to frontal type storms.
As long as any point measurement inaccuracies are
consistently biased in one direction, the forecasts can be
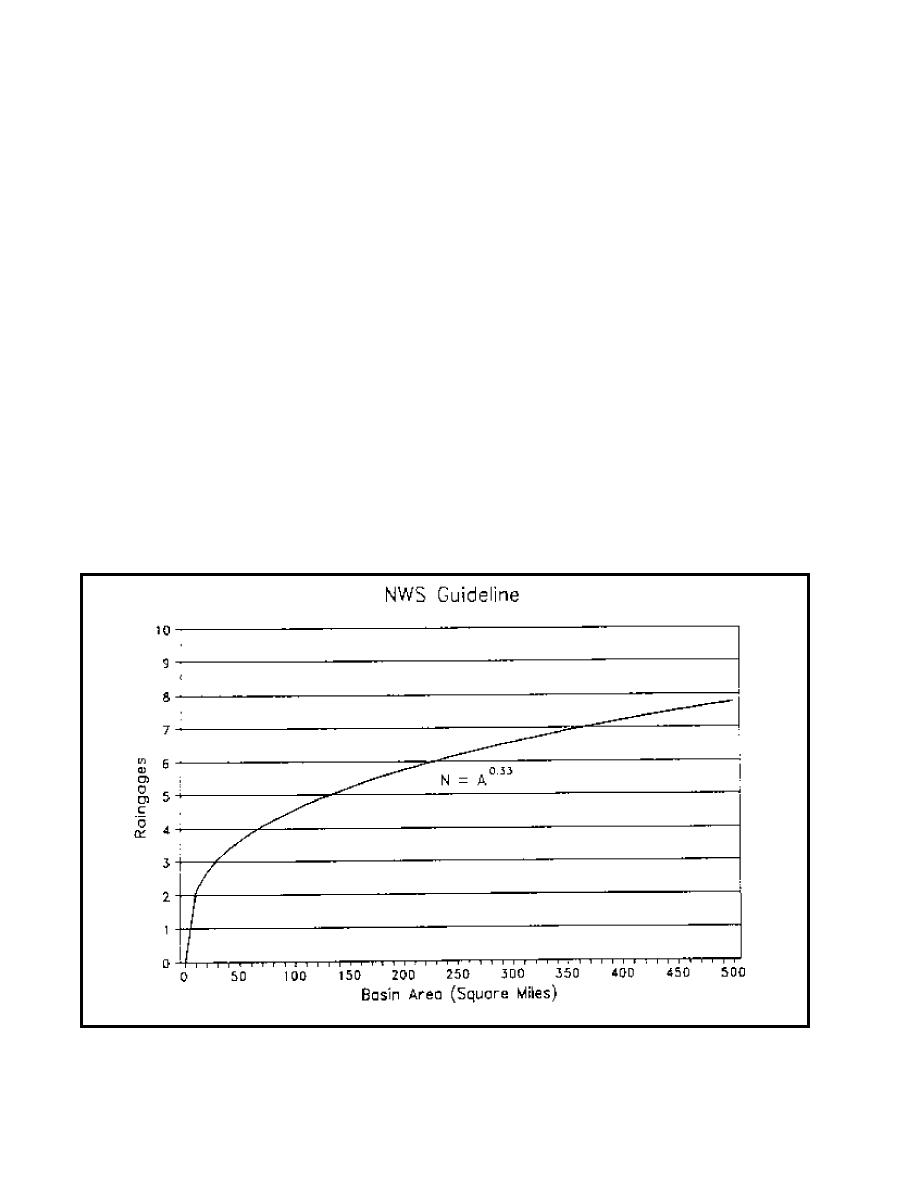
National Weather Service guidelines recommend a
!
quantitatively or qualitatively calibrated to account for the
minimum of three raingages and often use the follow-
bias.
ing relationship between the minimum number of
gages required (N) and the watershed area (A) in
(a) Number of gages. he number of raingages installed
square miles (Schaake 1980).
in a data collection system directly effects the quality of the
data and the performance of hydrologic forecast models. The
(4-1)
N ' A 0.33
(N > 3)
density of required raingages is based on the ability to provide
an accurate estimate of the mean areal precipitation for the
Equation 4-1 is shown graphically in Figure 4-1 and illustrates
watershed. The minimum number is usually considered to be
how the minimum number of gages increases rapidly for areas
three gages. The maximum number is generally governed by
#129.5 sq km (50 sq miles).
the resources available and whether additional increases in flood
warning time and reliability can be realistically achieved by
increasing the gage density. Additional gages are often
implemented in stages as more is learned about the system.
Figure 4-1. Minimum raingage network size
4-2




 Previous Page
Previous Page
