ETL 1110-1-175
30 Jun 97
performed by the interactive kriging software
described in Grundy and Miesch (1987).
4-2. General Computation of Empirical
Variogram
a. As described in section 2-3, the variogram
((h) characterizes the spatial continuity of a
regional variable for pairs of locations as a func-
tion of distance or lag h between the locations.
This variogram is sometimes called the theoretical
variogram because it is assigned a continuous
functional form that expresses the spatial correla-
tion for any lag in the region of analysis. The
function is estimated by fitting one of the equations
given in section 2-3 to empirical or sample vario-
8
gram points ((h) using data whose locations con-
8
tribute only a finite number of lags. Although ((h)
characterizes the spatial correlation of the data, it
is computed from residuals of the data off the spa-
tial mean. Therefore, without prior knowledge of
nonstationarity in the underlying spatial process,
the first step in computing the sample variogram is
to identify existing nonstationarity indicated for the
spatial mean.
b. The approximation to Equation 2-19
2
begins by computing squared differences Di, j from
the data values z(xi), z(x2), ...z(xn) collected at loca-
tions x1, x2, ... xn
2
(4-1)
2
Di, j = z (x ) & z (x )
i
j
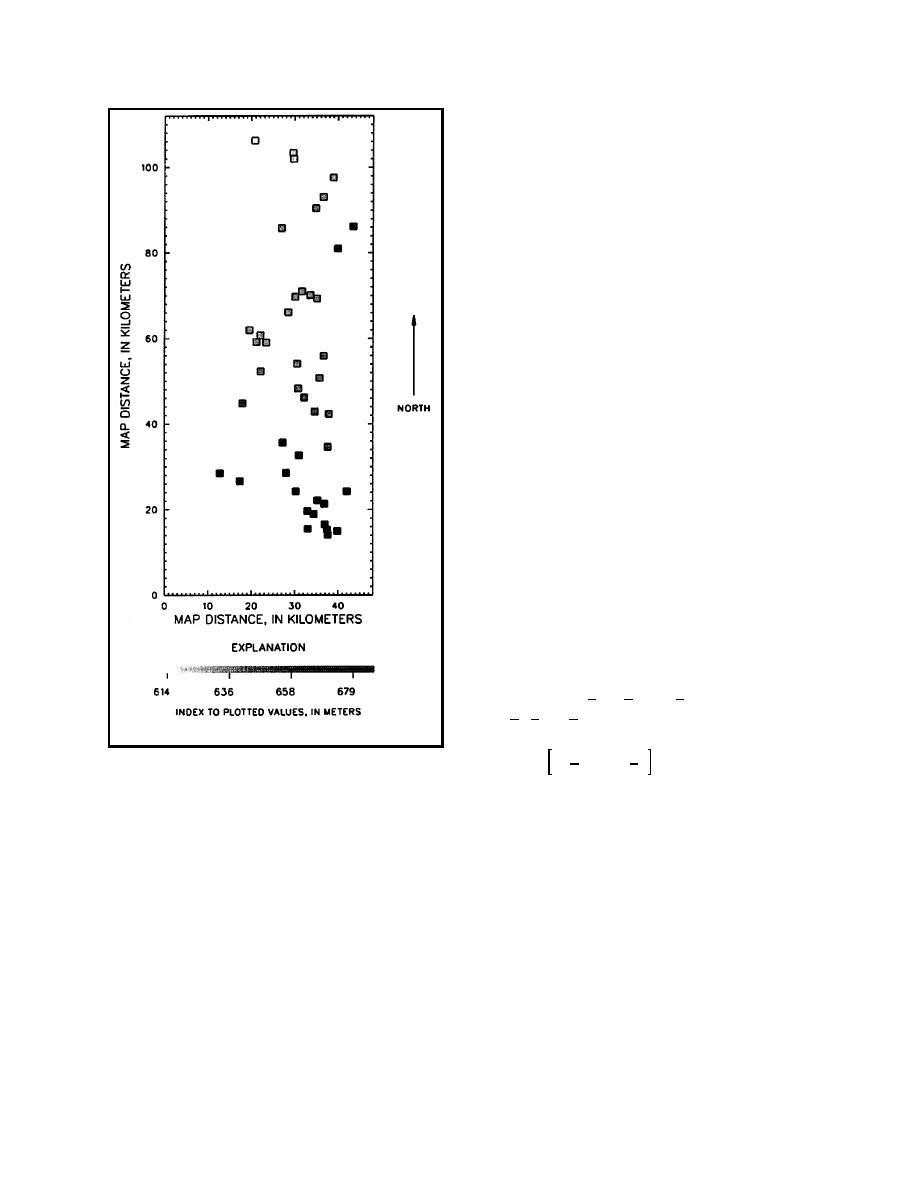
Figure 4-1. Measured water levels from Saratoga
data
If the spatial mean is stationary, then the squared
differences of the data are equivalent to the
stationary; if the mean changes with location, then
squared differences of the residuals, and sample
it is spatially nonstationary. Generally, if the data
variogram computations can be continued using
have a stationary spatial mean, the discussions in
the data themselves. If the spatial mean is strongly
sections 4-3 and 4-7, which address nonstation-
nonstationary, the plot of Equation 4-1 versus the
arity and additional trend considerations, can be
distance between associated points may indicate a
omitted. If the spatial mean is not stationary, as
trend or drift that would need to be removed before
for this example data set, then sections 4-3 and 4-7
further variogram computations could be made.
become important, and the sequence of stages for
Drift would have to be considered in HTRW
obtaining a variogram becomes an iterative pro-
studies, such as determining contaminant concen-
cedure. All variogram and kriging computations
trations areally dispersed from localized sources or
for the Saratoga groundwater levels example were
4-2



 Previous Page
Previous Page
