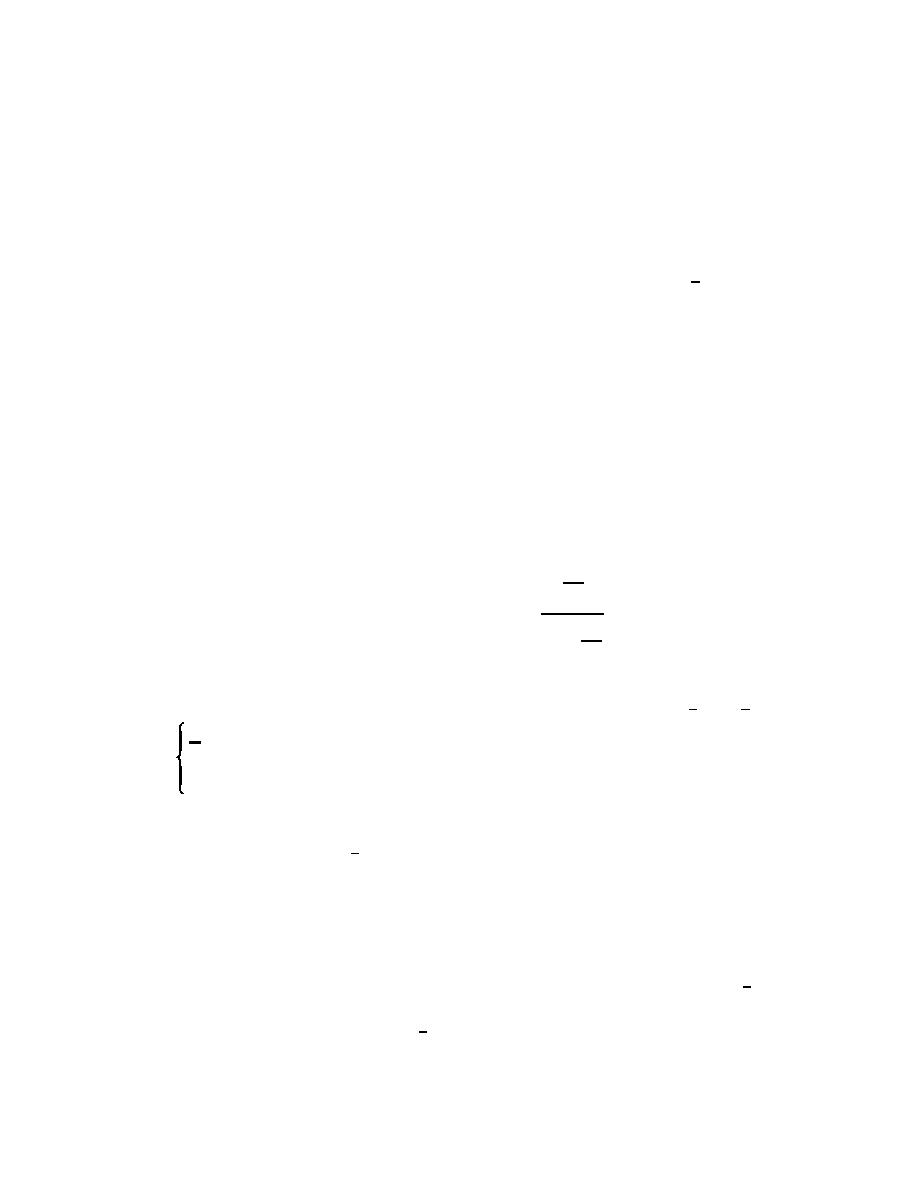
ETL 1110-1-175
30 Jun 97
k = 1, the predictor is an exact interpolator and is
This predictor represents the smoothest possible
predictor surface. In using this predictor, a certain
constant on the Voronoi polygons (see section 7-5)
degree of spatial homogeneity is assumed. No
induced by the measurement locations.
attempt is made to incorporate any detectable
c. There are several variations of this pre-
patterns (or trends) in the mean or variance of the
data as a function of location, and the fact that
dictor. In one such variation, a distance r may be
fixed (rather than fixing k) and averages over loca-
measurements made at points that are close to each
tions that are within distance r of x0 taken. Addi-
other may be related is disregarded. Such a pre-
dictor has the advantage of being very simple to
tionally, a moving-median may be used rather than
compute; it needs no estimation of a variogram or
a moving average. Sorting and testing distances
other model parameters. The disadvantage is that
can slow computations relative to obtaining the
representing the spatial field by a single value
simple average, and use of medians rather than
ignores much of the relevant and interesting struc-
means leads to a more resistant (to outliers)
ture that may be very helpful in improving
predictor.
predictions.
b. As discussed in section 2-4, if applied in a
7-4. Inverse-Distance Squared Weighted
Average
stochastic setting, this predictor would be optimal
(best linear unbiased) if there is no drift and if
a. The weights wi are (Journel and Huijbregts
residuals are uncorrelated and have a common
variance.
1978)
1
7-3. Simple Moving Average
hi2
0
wi =
(7-4)
j
n
a. Let hi0 be the distance of x0 from xi, let h[i0]
1
be the ordered (from smallest to largest) distances,
2
hj0
j=1
and fix 1 # k # n. Then the weights wi are
(Cressie 1991)
where again hi0 is the distance of x0 from xi.
1
, h # h[k 0]
b. In the simple moving average, weights are
k i0
wi =
(7-3)
the same, provided measurement locations are
0, hi0 > h[k 0]
sufficiently close to the prediction location and are
zero otherwise. For the inverse-distance squared
method, weights are forced to decrease in a
Thus, this predictor is the average of the measure-
smoother manner as distance from the prediction
ments at the k nearest locations from x0.
location increases. This predictor again has the
advantage of being easy to compute. Another
b. If k is equal to n, this predictor is identical
feature of this predictor is that it is an exact inter-
to the simple average, with weights as given in
polator. In addition, the exponent 2 of hi0 may be
Equation 7-2. A choice of k smaller than n reflects
changed to any positive number, giving the user
an assumption that the predictor needs to incor-
some flexibility in determining the rate of decrease
porate more of the local fluctuation observed in the
of weights as a function of distance from x0. Isaaks
data, or, equivalently, that measurements at loca-
and Srivastava (1989, pp. 257-259) present an
tions near x0 should be more informative than
example illustrating the effects on weights of
measurements at other locations in predicting z(x0);
changing the exponent.
the smaller k is, the more variable the predictor. If
7-2



 Previous Page
Previous Page
