ETL 1110-2-560
30 Jun 01
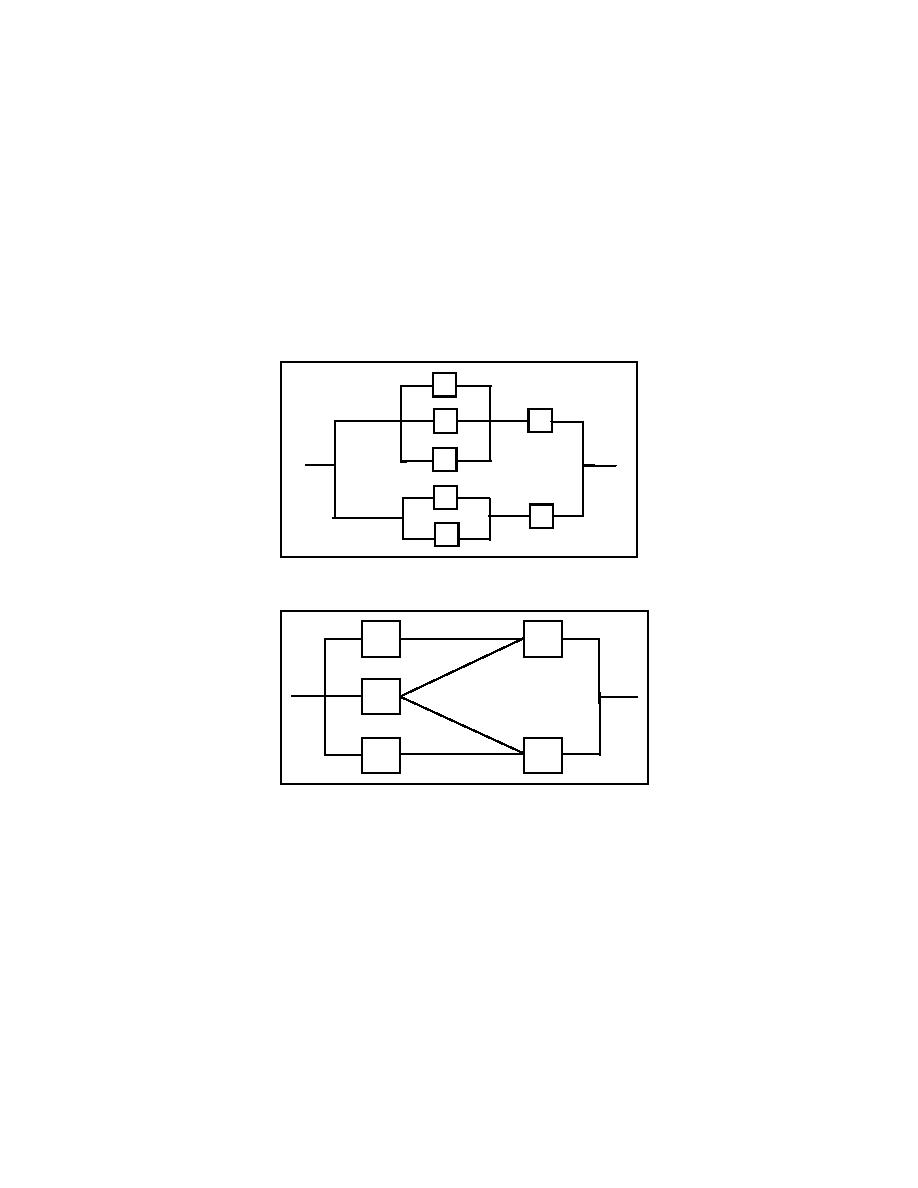
(3) Complex system models. Complex systems can be represented as a series-parallel combination or
a non-series-parallel configuration. A series-parallel RBD is shown in Figure 9. This type of system is
analyzed by breaking it down into its basic parallel and series modules and then determining the
reliability function for each module separately. The process can be continued until a reliability function
for the entire system is determined. The reliability function of Figure 9 would be evaluated as follows:
R1(t) = ( 1 {[1 - RA1(t)] [1 - RB1(t)] [1 - RC1(t)]}) * RD1(t)
(19)
R2(t) = ( 1 {[1 - RA2(t)] [1 - RB2(t)]}) * RD2(t)
(20)
RS(t) = ( 1 {[1 - R1(t)] [1 - R2(t)]})
(21)
A1
B1
D1
C1
A2
D2
B2
Figure 9. Series-parallel system
B1
C1
A
C2
B2
Figure 10. Non-series-parallel system
A non-series-parallel system is shown in Figure 10. One method of analyzing non-series-parallel systems
uses the following general theorem:
RS(t) = RS(if X is working) RX(t) + RS(if X fails) [1- RX(t)]
(22)
The method lies in selecting a critical component (X) and finding the conditional reliability of the system
with and without the component working. The theorem on total probability is then used to obtain the
systems reliability (see Appendix G).
11



 Previous Page
Previous Page
