ETL 1110-2-563
30 Sep 04
(4) Second, the model was based on crushing of the barge corner. Such large deformations are very
rarely encountered on the inland waterway during most usual and unusual impact events.
(5) Third, the model utilized a trigonometric function to represent the stiffness function; the function
yielded incorrect results for small approach angles (less than 5 degrees) and large angles (greater than 85
degrees). Therefore, this model did not yield realistic results for head-on impacts into bullnoses and
protection cells and for estimating the resulting impact forces at small angles. The limitations of this
model were primarily the result of applying technology that is appropriate for deep-draft vessels to inland
barge trains without field validation. The limitations of the model, combined with the consensus that the
model produces conservative design loads, are the primary reasons why USACE performed prototype
(Patev, Barker, and Koestler 2003b) and full-scale (Patev, Barker, and Koestler 2003a) barge impact
experiments as a basis for improving this method.
b. Objectives. This ETL provides the following:
Information for estimating the masses, approach velocities, and approach angles. Examples of
data and distributions for mass, angle, and velocity from recent designs of USACE navigation
projects structures are shown in Appendix C.
Information on return periods for use in probabilistic design of lock walls for barge impact loads
are explained through examples in Appendix D.
A new empirical method (Arroyo, Ebeling, and Barker 2003) for estimating corner impact loads
on rigid walls is furnished in Appendix E. This method is based on the results of full-scale
experiments described in Appendix F (Patev, Barker, and Koestler 2003a, 2003b).
B-2. Empirical Barge Impact Model
a. Full-scale barge impact experiments were conducted from
Fm
1997 to 2000. These experiments were performed to increase
understanding of the complex dynamics and failure modes of the
barge train system, and to assist in the development of numerical
models. No barge damage or lashing failures occurred during the
impacts used to develop the empirical correlation. This is not
V0y
consistent with the Minorsky (1959) model discussed in ETL 1110-
2-338. The data used to derive the empirical correlation were
M
limited to barge train velocities up to 0.17 m/sec (0.57 ft/sec)
normal to the wall, for impact angles up to 21.1 deg, and for linear
momentum normal to the wall between 2.9 and 4.6 MN-sec (650
θ
and 1,025 k-sec). In addition, the experiments indicated that an
V0x
MDOF system must be used to model the barge train to account for
the dynamic response of the lashings. Further details on the experi-
ments and their results are described in Appendix F.
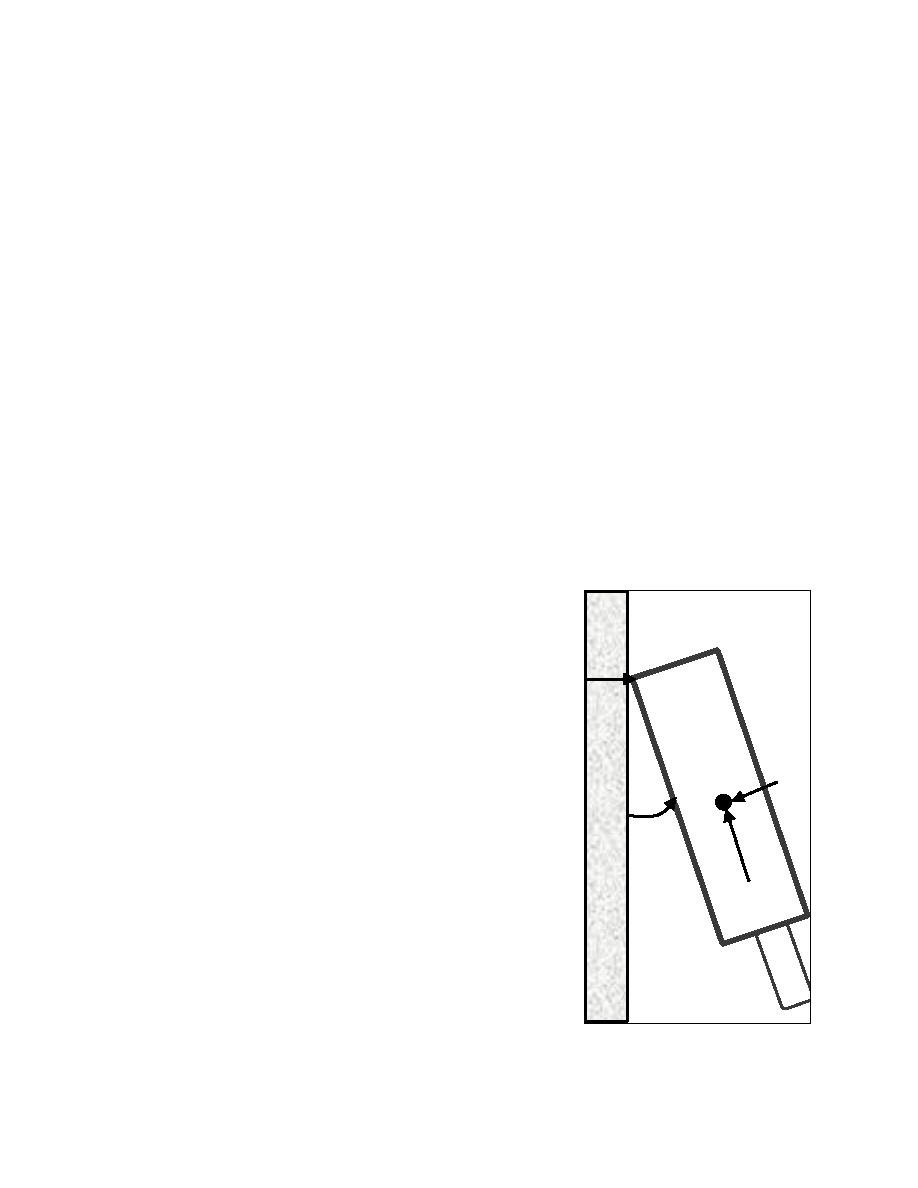
b. Based on the results (Patev, Barker, and Koestler 2003a)
and processing of the experiments (Arroyo, Ebeling, and Barker
2003), an empirical correlation has been developed to equate the
maximum impact force normal to the wall Fm to the linear momen-
tum of the barge train as it impacts the wall. Figure B-5 shows the
data required for the empirical correlation. The results from the
Figure B-5. Data requirements
for empirical model
B-3



 Previous Page
Previous Page
