ETL 1110-2-547
30 Sep 95
As the second-order terms are small when the coeffi-
cients of variation are not exceedingly large (below
approximately 30 percent), the equation above is
sometimes approximated as:
EC
E ln FS . ln E C & ln E D ' ln
ED
The standard deviation of the log of the factor of
safety is obtained as:
Fln FS ' F 2n C % F2n D
l
l
Fln FS '
2
2
ln 1 % VC % ln 1 % VD
Introducing an approximation,
2
2
ln 1 % VC ' . VC
the reliability index for lognormally distributed C, D,
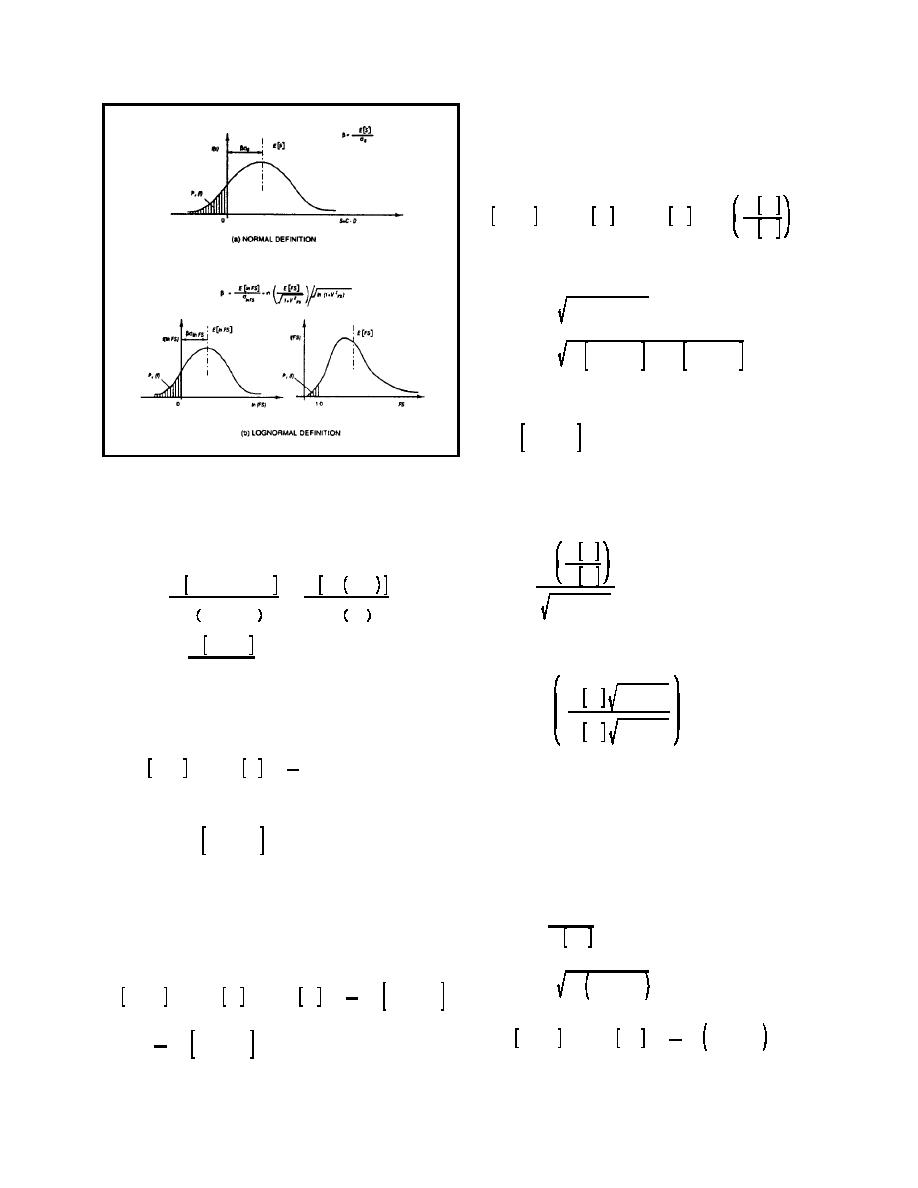
Figure B-2. Alternative definitions of the reliability index
and FS and normally distributed ln C, ln D, and ln FS
can be expressed approximately as:
exceeds zero in terms of the standard deviation of
ln FS, it is:
EC
ln
ED
E ln C & ln D
E ln C/D
$'
$'
'
2
2
VC % VD
F ln C & ln D
Fln C/D
E ln FS
The exact expression is:
'
Fln FS
2
EC
1 % VD
b. From the properties of the lognormal
$ ' ln
distribution, the expected value of ln C is:
2
ED
1 % VC
1 2
F
E ln C ' ln E C &
For many geotechnical problems and related deter-
2 ln C
ministic computer programs, the output is in the form
where:
of the factor of safety, and the capacity and demand
are not explicitly separated. The reliability index must
F2n C ' ln 1 % VC
2
be calculated from values of E[FS] and FFS obtained
l
from multiple runs as described in the next section. In
this case, the reliability index is obtained using the
following steps:
FFS
c. The expected value of the log of the factor of
VFS '
safety is then:
E FS
Fln FS '
2
ln 1 % VFS
1
2
E ln FS ' ln E C & ln E D &
ln 1 % VC
2
1
2
E ln FS ' ln E FS &
ln 1 % VFS
1
2
ln 1 % VD
%
2
2
B-7


 Previous Page
Previous Page
