ETL 1110-2-547
30 Sep 95
with the partial derivatives taken at the expansion point
2
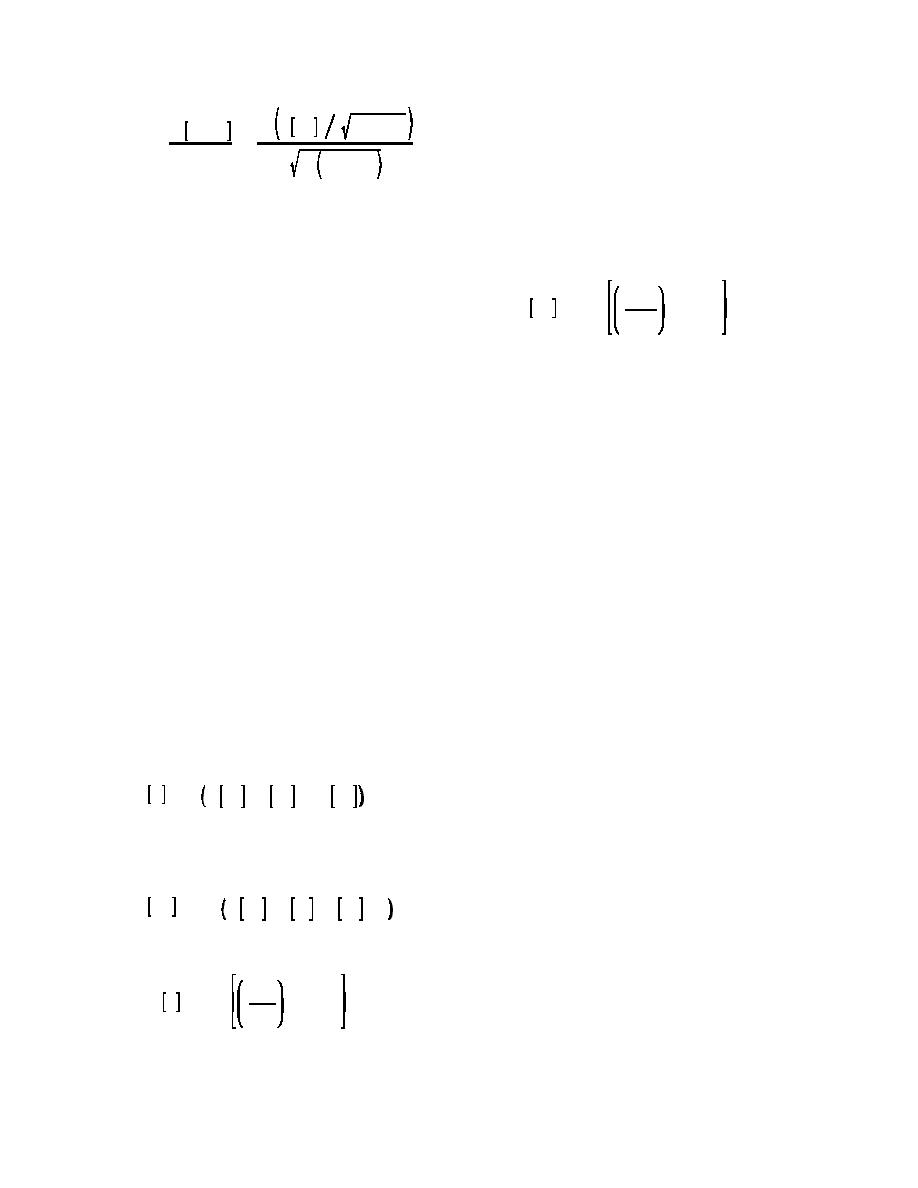
ln E FS
1 % VFS
E ln FS
(in this case the mean or expected value). Using the
$'
'
factor of safety as an example performance function,
Fln FS
2
ln 1 % VFS
the variance is obtained by finding the partial deriva-
tive of the factor of safety with respect to each random
variable evaluated at the expected value of that varia-
ble, squaring it, multiplying it by the variance of that
random variable, and summing these terms over all of
B-8. Integration of the Performance Function
the random variables:
Methods such as direct integration, Taylor's series
method, point estimate method, and Monte Carlo
Var FS ' j
2
M FS
Var Xi
simulation are available for calculating the mean and
M Xi
standard deviation of the performance function. For
direct integration, the mean value of the function is
obtained by integrating over the probability density
The standard deviation of the factor of safety is then
function of the random variables. A brief description
simply the square root of the variance.
of the other methods follows. The references should
be consulted for additional information.
(a) Having the expected value and variance of the
factor of safety, the reliability index can be calculated
a. Taylor's series method. Taylor's series
as described earlier in this appendix. Advantages of
method is one of several methods to estimate the
the Taylor's series method include the following:
moments of a performance function based on moments
of the input random variables. It is based on a Taylor's
The relative magnitudes of the terms in the
series expansion of the performance function about
above summation provide an explicit indica-
some point. For the Corps' navigation rehabilitation
tion of the relative contribution of uncertainty
studies, the expansion is performed about the expected
of each variable.
values of the random variables. The Taylor's series
method is termed a first-order, second-moment
The method is exact for linear performance
(FOSM) method as only first-order (linear) terms of
functions.
the series are retained and only the first two moments
(mean and the standard deviation) are considered. The
Disadvantages of the Taylor's series method include
method is summarized below.
the following:
(1) Independent random variables. Given a
It is necessary to determine the value of
function Y = g(X1, X2, ... Xn), where all Xi values are
derivatives.
independent, the expected value of the function is
obtained by evaluating the function at the expected
The neglect of higher order terms introduces
values of the random variables:
errors for nonlinear functions.
E Y ' g E X1 , E X2 , ... E Xn
(b) The required derivatives can be estimated
numerically by evaluating the performance function at
two points. The function is evaluated at one increment
For a function such as the factor of safety, this implies that
above and below the expected value of the random
the expected value of the factor of safety is calculated
variable Xi and the difference of the results is divided
using the expected values of the random variables:
by the difference between the two values of Xi.
Although the derivative at a point is most precisely
E FS ' FS E N1 , E c1 , E (1 , ...
evaluated using a very small increment, evaluating the
derivative over a range of plus and minus one standard
The variance of the performance function is taken as:
deviation may better capture some of the nonlinear
behavior of the function over a range of likely values.
Thus, the derivative is evaluated using the following
Var Y ' j
2
MY
Var Xi
approximation:
M Xi
B-8


 Previous Page
Previous Page
