ETL 1110-1-175
30 Jun 97
without bound as the lag increases, a regionalized
random variable with a linear variogram will have
ever-increasing variability about its mean as the
size of the sampling region is increased. In appli-
cations involving the linear variogram, the vario-
gram is usually truncated at a sill corresponding to
the value of the variogram at maximum lag hmax.
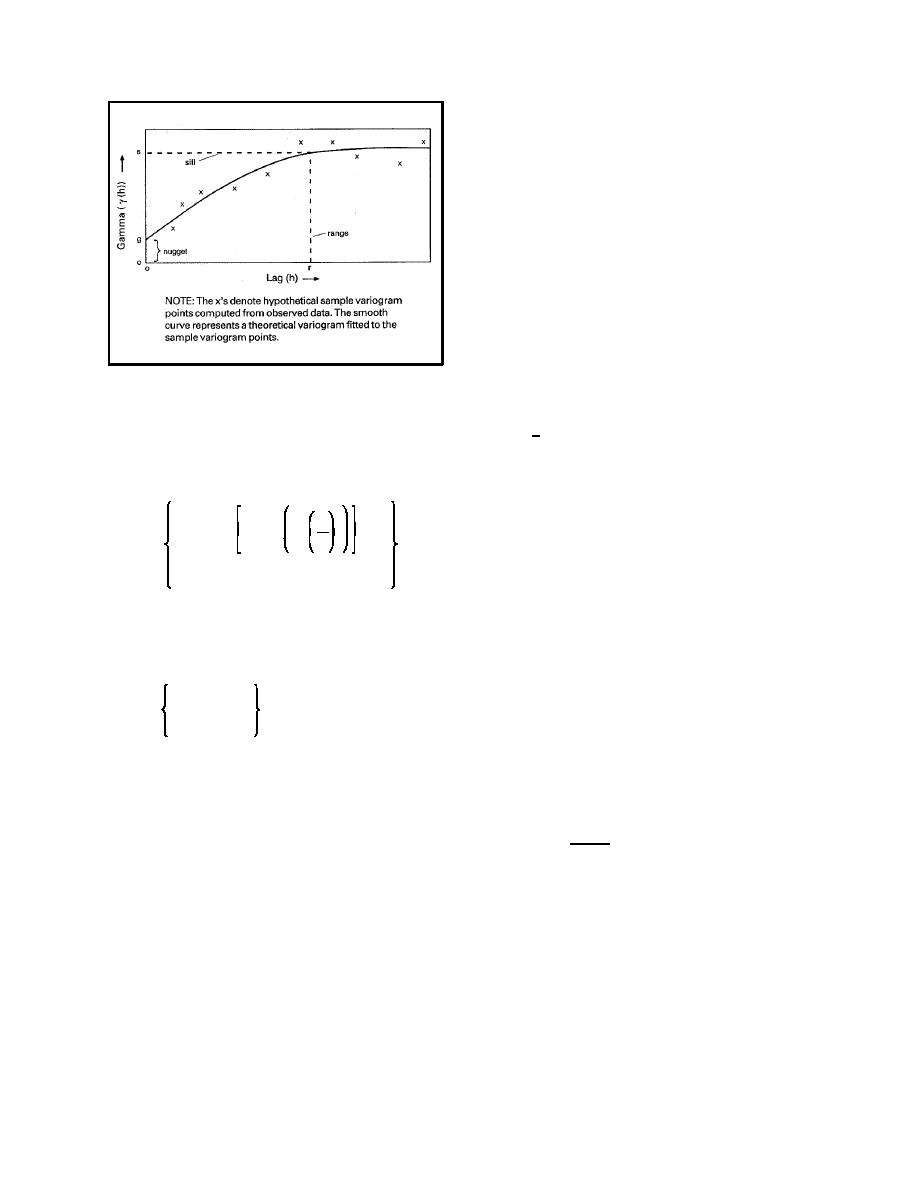
g. Before closing this section, it will be use-
ful to highlight some similarities and contrasts
between the covariance function and the vario-
gram. Although the variogram is commonly used
in a geostatistical analysis, it is sometimes easier to
gain an intuitive understanding of the methodology
using the covariance function, or equivalently, the
Figure 2-2. Diagram showing variogram and features
spatial variance and the correlation function.
When Z(x) has a stationary, isotropic covariance
the Gaussian variogram (parameters: sill, s > 0;
function (Equation 2-9), there is a one-to-one
nugget, 0 < g < s; range, r > 0)
correspondence between the variogram and the
covariance function, namely
2
h
(2-27)
( (h) = C (0) & C (h)
, h>0
g % (s & g) 1 & exp &3
( (h) =
(2-25)
r
As long as C(h) approaches zero as h increases (a
h=0
0,
minor technicality that can always be assumed in
practice), then, as indicated by Equation 2-27, the
and, the linear variogram (parameters: nugget,
variogram reaches a sill and the sill equals C(0).
g > 0; slope, b > 0)
Therefore, when dealing with a covariance-
stationary regionalized random variable, the vario-
g % bh, h > 0
gram and the spatial covariance function contain
(2-26)
( (h) =
the same information as one another. By factoring
h=0
0,
out C(0)=s from Equation 2-27 and using Equa-
tion 2-14, the relationship between the spatial
f. Although there are many other models that
correlation function and the variogram can be
are used for variograms (Journel and Huijbregts
obtained
1978), these four are the most commonly used and
are shown in Figure 2-3. The exponential, spheri-
( (h)
D (h) = 1 &
(2-28)
cal, and Gaussian models are similar in that they
s
all have a sill and a range. However, they have
different shapes near zero lag (h=0) that, as will be
From Equation 2-28, it is evident that high values
discussed in Chapter 4, result in significant differ-
of ((h) (i.e., close to s) signify low values of D(h).
ences in the prediction results using the three
In fact, D(h) = 0 whenever ((h) = s, indicating that
models. The linear model is quite different from
observations whose locations are farther apart than
the other three, in that it does not reach a sill, but
the range are uncorrelated. As h gets small, a
increases linearly without. This fact will have
nugget in ((h) is reflected in a correlation that is
important implications on the prediction results
less than 1
using a linear variogram. Because the squared
differences between residuals tend to increase
2-8



 Previous Page
Previous Page
