ETL 1110-1-175
30 Jun 97
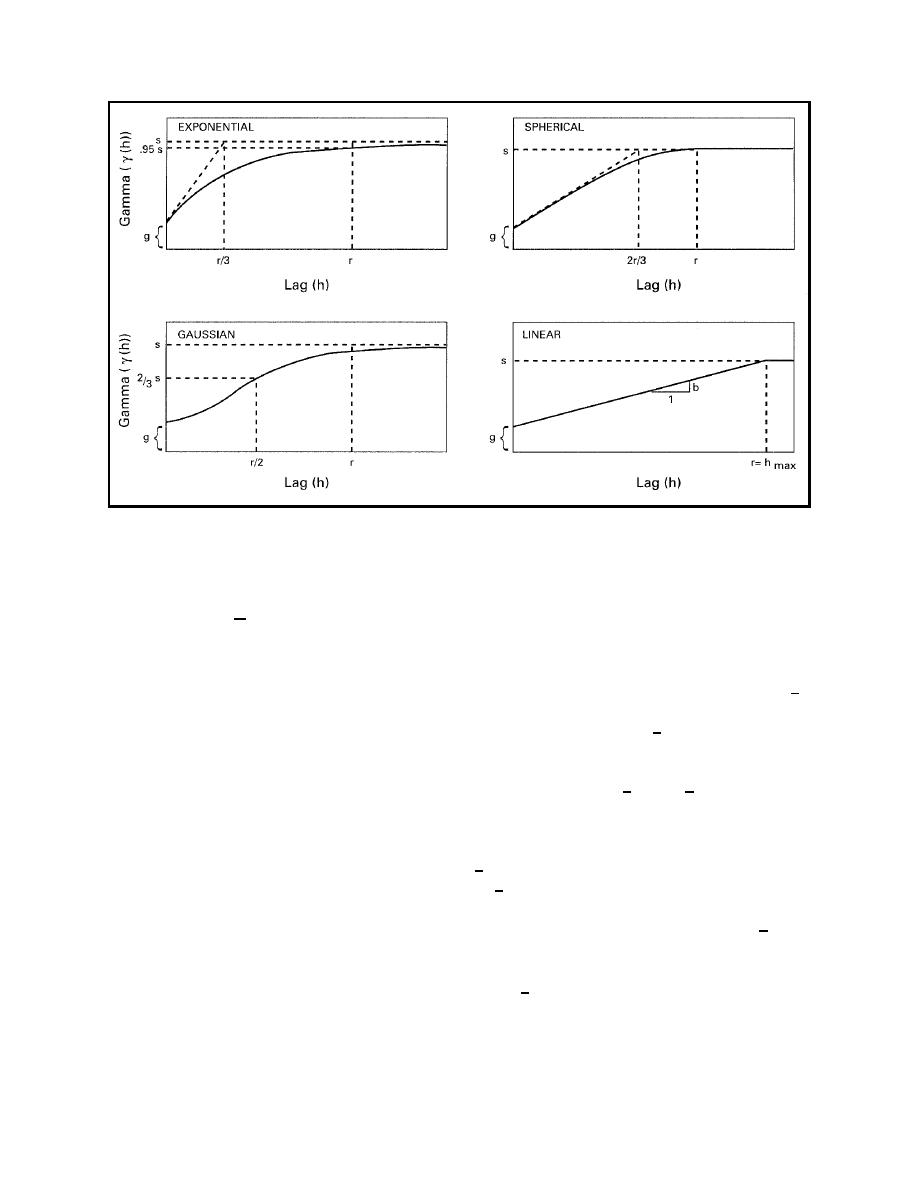
Figure 2-3. Theoretical variograms showing A, exponential; B, spherical; C, Gaussian; and D, linear
models
61&
60
2-4. Kriging
g
D (h)
(2-29)
as h
s
a. General.
Therefore, the larger g is in relation to s, the less
(1) Given a regionalized random variable Z(x)
correlated nearby observations are. The case when
with a known theoretical variogram, the question
g=s, called a pure nugget variogram, results in
is: how can the value of Z(x) be predicted at an
D(h)=0 for all h>0. In that case, neighboring
arbitrary location, based on measurements taken at
observations are uncorrelated no matter how
other locations? Suppose that Z is measured at n
closely they are spaced.
specified locations: Z(x1), ..., Z(xn). For example,
h. Occasionally, ((h) may not reach a finite
the locations might correspond to n preexisting
sill, as in the linear variogram Equation 2-26. In
wells in an aquifer. Let a new location be given by
that case, it is not possible to define a correlation
x0=(u0,v0) and denote the ith measurement location
function as in Equation 2-28. The corresponding
by xi=(ui,vi). Suppose that, based on prior knowl-
regionalized random variable is said to be intrinsi-
edge of the geology, there are no prevailing trends
cally stationary (Journel and Huijbregts 1978),
in hydraulic conductivity, so the mean of Z(x) is
which is more general than covariance stationarity.
assumed to be constant over the entire region:
The theory behind intrinsically stationary vario-
grams will not be presented in this ETL. As long
(2-30)
as a "pseudo-range" hmax is defined, all of the
(x) = (constant)
computations described below can be generalized.
2-9



 Previous Page
Previous Page
